白努利定律(Bernoulli's law)

是流體力學中的一個定律，由瑞士流體物理學家白努利於1738年出版他的理論《Hydrodynamica》，描述流體沿著一條穩定、非粘滯、不可壓縮的流線移動行為。
在流體動力學，白努利原理指出，無粘流的流體的速度增加發生同時與一個減少壓力或減少流體的潛在能量。
白努利原理可以應用到不同類型的流體流動，從而是可廣泛套用的白努利方程式表示式。事實上，有不同類型的流的白努利方程式的不同形式的。白努利原理的簡單形式是有效的不可壓縮流動（如最液體流動），也為移動可壓縮流體（如氣體）在低馬赫數（通常小於0.3）。更先進的形式可被應用到在某些情況 ​​下，在更高的馬赫數（見白努利方程式的推導）可壓縮流。
白努利原理可以從能量守恆的原則。這說明，在一個穩定的流量，在所有點上，簡化各種形式的流體機械能沿著流線型的總和是相同的。這就要求，動能和勢能的總和保持不變。因此，一個增加的速度的流體發生動態壓力和動能，並在其靜態壓力和勢能減少成比例的增加。如果液體流出水庫，各種形式的能量的總和是相同的，都簡化了，因為每單位體積的能量的總和（壓力和重力潛在ρGH）是在水庫到處都是一樣的。
白努利原理，也可以直接來自牛頓第二定律。如果一個小體積區域的流體的水平流動，然後沿著流動方向，有從高壓到低壓的分佈，後方區域自然比前面區域有更多的壓力。假設前後方區域面積相等，如此便提供了一個正方向淨力施於原先設定的流體小體積區域，加速其沿正方向流動。
流體粒子只受到壓力和自己的體重重力之影響。如果流體是流動的水平方向和沿流線的截面，其中的速度增加只能是因為在該部分上的流體已經從較低壓力的區域的較高壓力的區域移動，如果它的速度降低，只能是因為它已經從較低的壓力更高的壓力的區域的區域。因此，在流動的流體的水平之內，以最高的速度發生壓力最低，最低的速度發生壓力最高。
一、原表達形式

流動速度
地心加速度(地球)
流體處於的高度(從某參考點計)
流體所受的壓強
流體的密度
常數
二、定理假設（Assumptions）
使用白努利定律必須符合以下假設，方可使用；如沒完全符合以下假設，所求的解也是近似值。
定常流（或稱穩定流，Steady flow）：在流動系統中，流體在任何一點之性質不隨時間改變
不可壓縮流（Incompressible flow）:密度為常數，在流體為氣體適用於馬赫數(M)<0.3
無摩擦流（Frictionsless flow）:摩擦效應可忽略，忽略黏滯性效應
流體沿著流線流動（Flow along a streamline）:流體元素（element）沿著流線而流動，流線間彼此是不相交的
三、推論過程

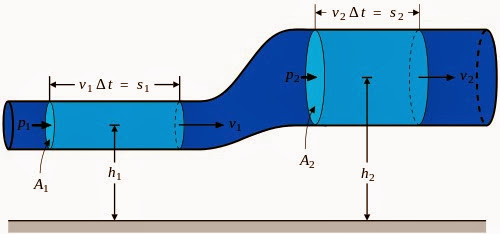
資料來源：維基百科

▼循環(circulation) 顯示/隱藏(show/hide)